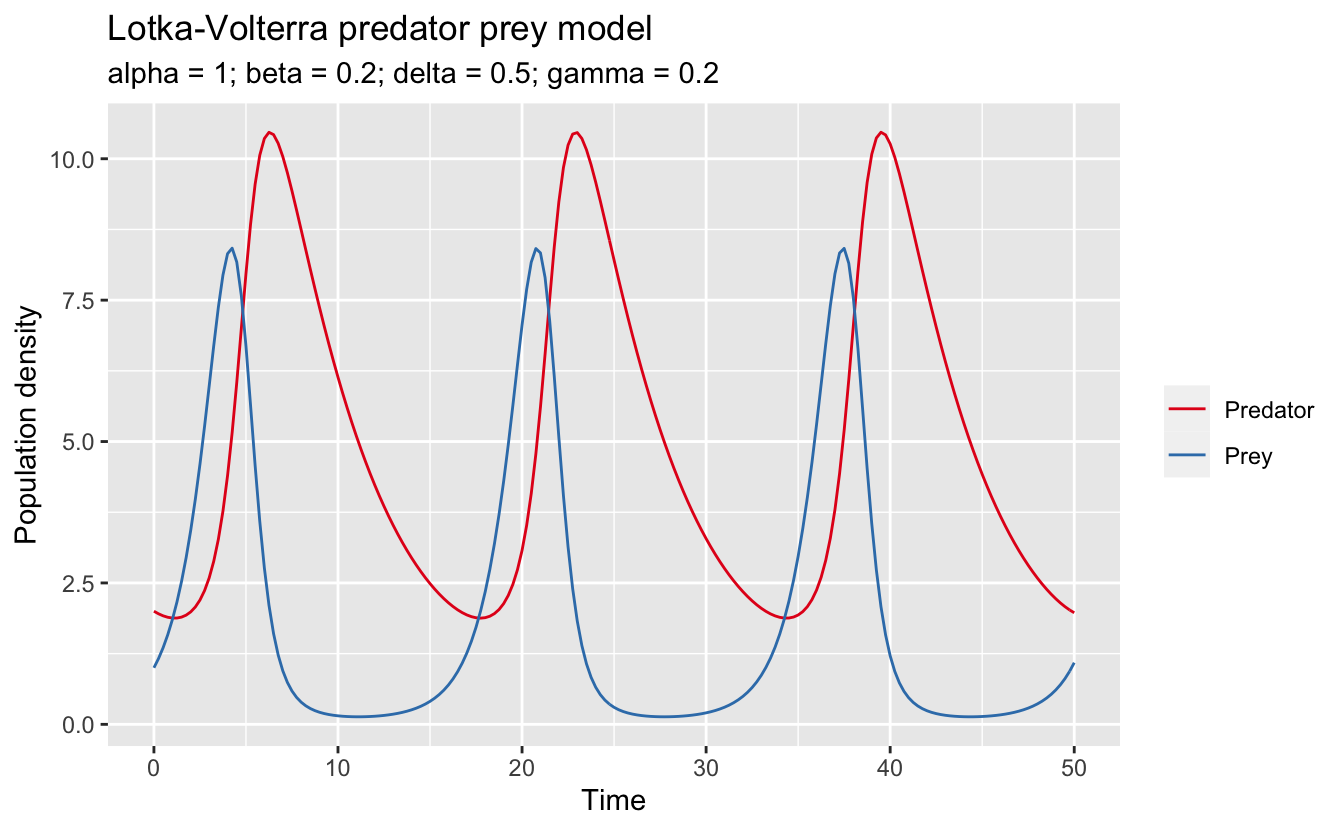
PPT An introduction to preypredator Models PowerPoint Presentation

LotkaVolterra Predator Prey Model Matt StrimasMackey

Introduction: The Lotka-Volterra model is composed of a pair of differential equations that describe predator-prey (or herbivore-plant, or parasitoid-host) dynamics in their simplest case (one predator population, one prey population). It was developed independently by Alfred Lotka and Vito Volterra in the 1920's, and is characterized by oscillations in the population size of both predator and.

Plot of predator and prey populations for the LotkaVolterra model

The Lotka-Volterra equations, also known as the Lotka-Volterra predator-prey model, are a pair of first-order nonlinear [disambiguation needed] differential equations, frequently used to describe the dynamics of biological systems in which two species interact, one as a predator and the other as prey. The populations change through time according to the pair of equations:

PredatorPrey Model (LotkaVolterra equations) YouTube

The predator-prey cycle demonstrates how populations of predators and prey interact and influence each other's growth. As predator numbers increase, prey populations decline, leading to a decrease in predators.. Go to differential equations and find Lotka - Volterra predator prey model (can use it in producer/consumer relations too.

LotkaVolterra predator prey model (PREDPREY). (a) system diagram

Prey-Predator Models. V. Křivan, in Encyclopedia of Ecology, 2008. The Functional and Numerical Response. The Lotka-Volterra model assumes that the prey consumption rate by a predator is directly proportional to the prey abundance. This means that predator feeding is limited only by the amount of prey in the environment.

The LotkaVolterra predatorprey model. This graph shows the efficiency

The Classical Lotka-Volterra Predator-Prey Model. In the classic Lotka-Volterra model, neither prey population nor predator population has an explicit carrying capacity. However, either or both may have an implicit carrying capacity imposed by the interaction between the two populations. To model the prey population, we begin with a basic.

Dynamics of a LotkaVolterra predatorprey system (a), with associated

Description of the Model The Lotka-Volterra equations were developed to describe the dynamics of biological systems. This system of non-linear differential equations can be described as a more general version of a Kolmogorov model because it focuses only on the predator-prey interactions and ignores competition, disease, and mutualism which the.

(PDF) Dynamics in a LotkaVolterra PredatorPrey Model with Time

The Prey-Predator model with linear per capita growth rates is \ [\dot x = (b - p y) x\] (Prey) \ [\dot y = (r x - d) y\] (Predators) This system is referred to as the Lotka-Volterra model: it represents one of the earliest models in mathematical ecology. Figure 2: Prey-Predator dynamics as described by the level curves of a conserved quantity.

(a) The standard LotkaVolterra predatorprey model results in

The Lotka-Volterra model of predator-prey dynamics is a mathematical framework used to study the interactions between populations of predators and their prey in ecological systems. It helps to understand the dynamics of population fluctuations and the stability of ecosystems over time. In this article, you can find Lotka-Volterra Model notes.

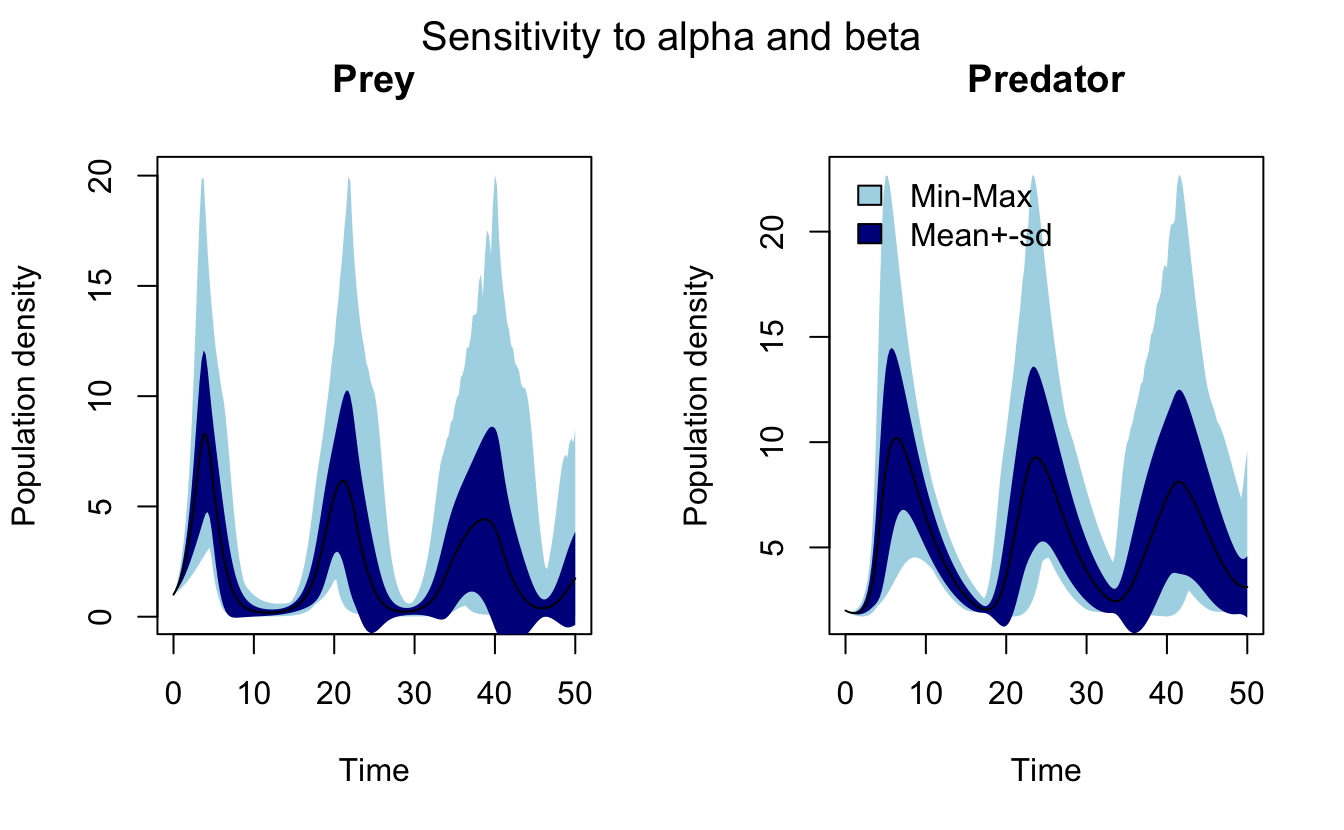
LotkaVolterra Predator Prey Model Matt StrimasMackey

The Lotka-Volterra equations describe an ecological predator-prey (or parasite-host) model which assumes that, for a set of fixed positive constants A (the growth rate of prey), B (the rate at which predators destroy prey), C (the death rate of predators), and D (the rate at which predators increase by consuming prey), the following conditions hold. 1. A prey population x increases at a rate.

PPT LotkaVolterra, PredatorPrey Model PowerPoint Presentation, free

Figure 3: Graphical view of the Lotka-Volterra model.. Thus far, we have focused on herbivore-plant interactions and predator-prey interactions, but parasites also play an important role in.

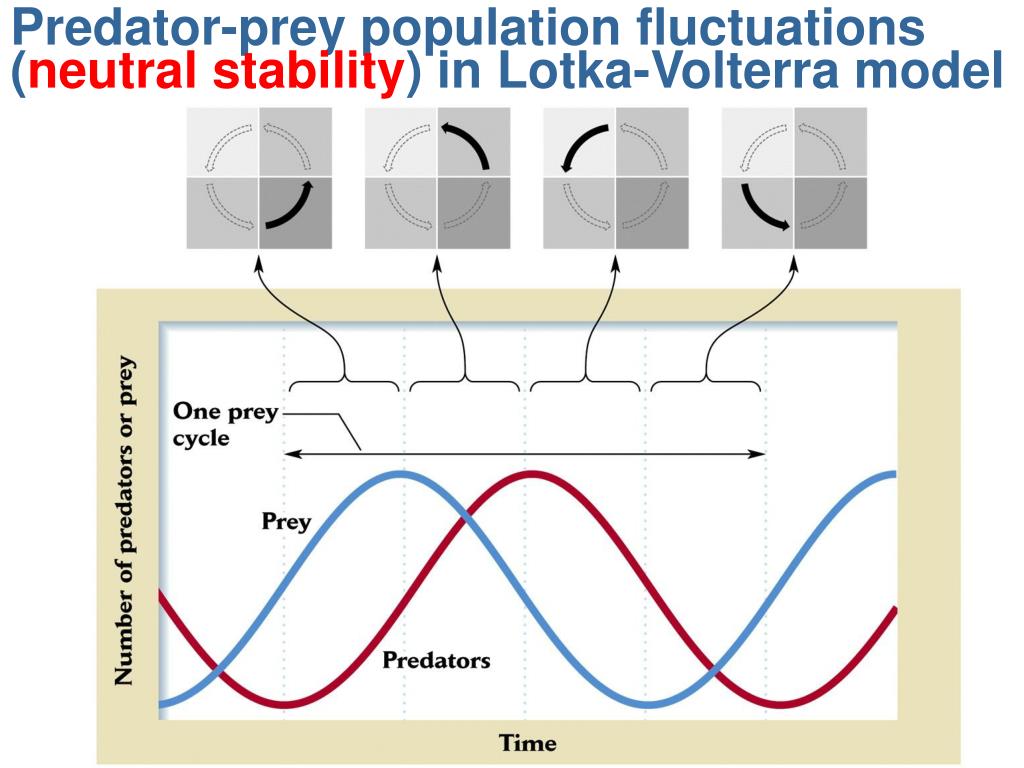
PPT Predatorprey interactions lecture content PowerPoint

Abstract. In 1920 Alfred Lotka studied a predator-prey model and showed that the populations could oscillate permanently. He developed this study in his 1925 book Elements of Physical Biology. In 1926 the Italian mathematician Vito Volterra happened to become interested in the same model to answer a question raised by the biologist Umberto d.

The Zcontrolled LotkaVolterra predator prey model basin of

This discussion leads to the Lotka-Volterra Predator-Prey Model: where a, b, c, and p are positive constants. The Lotka-Volterra model consists of a system of linked differential equations that cannot be separated from each other and that cannot be solved in closed form. Nevertheless, there are a few things we can learn from their symbolic form.

Lotka Volterra model Predator prey model with equation and Sample

The Lotka-Volterra model is the simplest model of predator-prey interactions. It was developed independently by: Alfred Lotka, an American biophysicist (1925), and. Vito Volterra, an Italian mathematician (1926). Basic idea: Population change of one species depends on: Its current population. Its reproduction rate.

PPT What does the LotkaVolterra model indicate about basic

the lotka-volterra predator-prey model This page titled 1.4: The Lotka-Volterra Predator-Prey Model is shared under a CC BY 3.0 license and was authored, remixed, and/or curated by Jeffrey R. Chasnov via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.

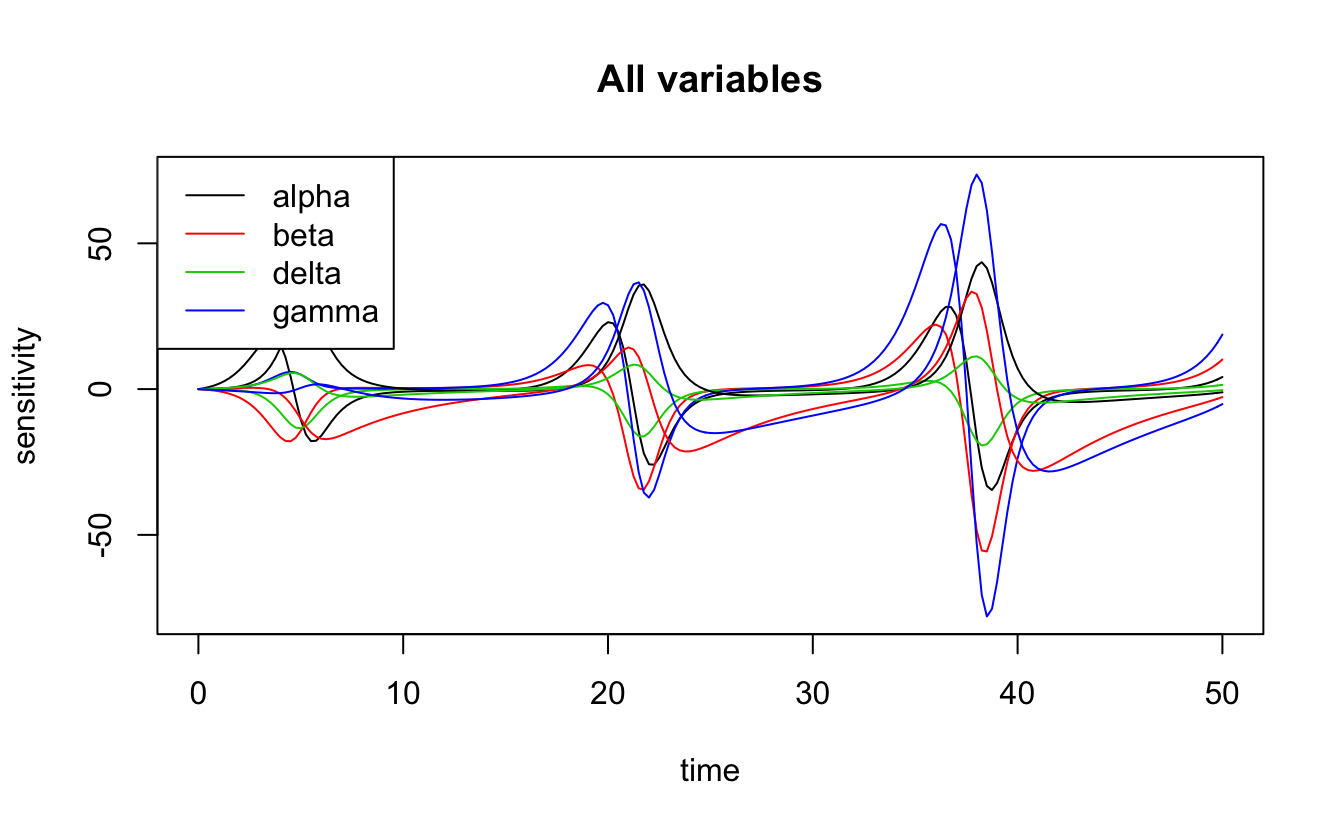
LotkaVolterra Predator Prey Model Matt StrimasMackey

The Lotka-Volterra model of interspecific competition builds on the logistic model of a single population. It begins with a separate logistic model of the population of each of the two, competing species. Population 1: dN1 dt = r1N1 ( K1 − N1 K1) d N 1 d t = r 1 N 1 ( K 1 − N 1 K 1) Population 2:

Solved Consider the LotkaVolterra predatorprey model

The. ecological Lotka-Volterra model describes the time evolution of two interacting populations via two simple, nonlinearly coupled, Ordinary Differential Equations (ODEs). It was introduced almost a century ago, presumably independently, by Alfred J. Lotka (1880- 1949) and Vito Volterra (1860-1940): the original papers are [1] [2], and.